La no transitividad de las relaciones de amistad (pese al consabido dicho de que los amigos de mis amigos son mis amigos), planteada hace un par de semanas, tiene una clara relación con la paradoja sorites. Puesto que, por pequeña que sea, siempre hay una “distancia” (de ideas, de carácter, de conducta…) entre dos personas. Por lo que una suma de proximidades puede convertirse en una distancia insalvable, del mismo modo que una tienda que está cerca de una tienda que está cerca de una tienda que está cerca de una tienda… que está cerca de tu casa, puede estar en la otra punta de la ciudad, si interponemos el suficiente número de cercanías.
En cuanto a los ocho problemas de la semana pasada, algunas respuestas rápidas o solo esbozadas y otras más detalladas:
1. Nos dicen que la mujer no es morena, y le contesta la persona de cabello rubio, por lo que ella ha de tener el cabello blanco, ergo…
2. En cuanto al triángulo obtusángulo a dividir en acutángulos, es fácil llegar a la falsa conclusión de que es imposible (Martin Gardner contaba que en su día recibió varias “demostraciones” de tal imposibilidad), pues por mucho que lo dividamos siempre acaba quedando al menos un pequeño y obstinado obtusángulo, como el del vértice inferior derecho de la figura.
Sin embargo, la división es posible y, como pista, diré que es uno de esos instructivos problemas en los que, inconscientemente, nos ponemos más condiciones de las que nos dicen que hay que cumplir. ¿Cuál es en este caso la condición inconsciente no pedida?
3. Los hermanos Marx eran cinco: Chico, Groucho, Harpo, Gummo y Zeppo; pero a efectos de nuestro acertijo, la solución más verosímil es que fueran cuatro (como en sus películas más famosas) y tres de ellos zurdos. La solución no es única: también podrían ser 21 hermanos y 15 de ellos zurdos. ¿Hay alguna solución más, aunque sea demográficamente inverosímil?
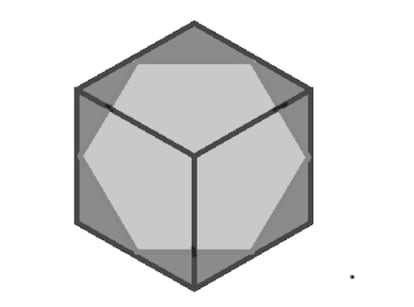
4. Si el plano de corte pasa por los puntos medios de seis de las aristas del cubo, obtenemos un hexágono regular.
5. 129 + 438 = 567 (¿Es única esta solución?).
6. Si OODDF es la raíz cuadrada de WONDERFUL, O no puede ser mayor de 2, pues entonces su cuadrado tendría diez cifras, y tampoco puede ser 1, pues el cuadrado de un número que empieza por 11 no puede tener un 1 en su segunda cifra; por tanto, O = 2. El número buscado estará, pues, entre los cuadrados de 22.000 y de 23.000, y puesto que el segundo dígito de WONDERFUL es 2, W = 5… Siguiendo esta línea de razonamiento, obtenemos WONDERFUL = 523.814.769.
7. La mayor circunferencia que pasa solo por casillas blancas tiene su centro en el centro de una casilla blanca y pasa por los vértices más distantes de las cuatro casillas negras que la rodean. (¿Cuál es su radio?).
8. Los trenes se aproximan a una velocidad relativa de 130 + 170 = 300 km por hora, por lo que 5 minutos antes de chocar estarán a 25 km uno de otro. La distancia inicial es irrelevante, solo sirve para despistar.
Juegos no transitivos
Con respecto a la no transitividad, comentó Salva Fuster: “Los dados no transitivos son uno de los casos más sorprendentes que conozco. Creo que la mayoría de las personas que ven dados no transitivos por primera vez, intentan buscar el error al contar los casos en los que cada dado gana a otro”. Muy cierto e interesante, tanto como para dedicarle al asunto una próxima entrega. Y para ir haciendo boca, piensa en algún otro juego no transitivo. Hay al menos dos muy populares…







